3. One Variable Equations #

Throughout this section and the next ones we shall cover the topic of solutions to one variable equations. Many different problems in physics and astronomy require the use of complex expressions, even with implicit dependence of variables. When it is necessary to solve for one of those variable, an analytical approach is not usually the best solution, because of its complexity or even because it does not exist at all. Different approaches for dealing with this comprehend series expansions and numerical solutions. Among the most widely used numerical approaches are the Bisection or Binary-search method, fixed-point iteration, Newton’s methods.

For further details see for example Chap. 5 of Ref. (1) or Chap. 4 of Ref. (3)

Contents

One Variable Equations

3.1. Bibliography #

[1] Kiusalaas, Numerical Methods in Engineering with Python
[2] Jensen, Computational_Physics. Companion repos: https://github.com/mhjensen Web page
[3] E. Ayres, Computational Physics With Python

%pylab inline
rc('animation', html='jshtml')

In /home/usuario/.local/lib/python3.6/site-packages/matplotlib/mpl-data/stylelib/_classic_test.mplstyle: 
The text.latex.preview rcparam was deprecated in Matplotlib 3.3 and will be removed two minor releases later.
In /home/usuario/.local/lib/python3.6/site-packages/matplotlib/mpl-data/stylelib/_classic_test.mplstyle: 
The mathtext.fallback_to_cm rcparam was deprecated in Matplotlib 3.3 and will be removed two minor releases later.
In /home/usuario/.local/lib/python3.6/site-packages/matplotlib/mpl-data/stylelib/_classic_test.mplstyle: Support for setting the 'mathtext.fallback_to_cm' rcParam is deprecated since 3.3 and will be removed two minor releases later; use 'mathtext.fallback : 'cm' instead.
In /home/usuario/.local/lib/python3.6/site-packages/matplotlib/mpl-data/stylelib/_classic_test.mplstyle: 
The validate_bool_maybe_none function was deprecated in Matplotlib 3.3 and will be removed two minor releases later.
In /home/usuario/.local/lib/python3.6/site-packages/matplotlib/mpl-data/stylelib/_classic_test.mplstyle: 
The savefig.jpeg_quality rcparam was deprecated in Matplotlib 3.3 and will be removed two minor releases later.
In /home/usuario/.local/lib/python3.6/site-packages/matplotlib/mpl-data/stylelib/_classic_test.mplstyle: 
The keymap.all_axes rcparam was deprecated in Matplotlib 3.3 and will be removed two minor releases later.
In /home/usuario/.local/lib/python3.6/site-packages/matplotlib/mpl-data/stylelib/_classic_test.mplstyle: 
The animation.avconv_path rcparam was deprecated in Matplotlib 3.3 and will be removed two minor releases later.
In /home/usuario/.local/lib/python3.6/site-packages/matplotlib/mpl-data/stylelib/_classic_test.mplstyle: 
The animation.avconv_args rcparam was deprecated in Matplotlib 3.3 and will be removed two minor releases later.

Populating the interactive namespace from numpy and matplotlib

JSAnimation import available at https://github.com/jakevdp/JSAnimation

#from JSAnimation import IPython_display
from matplotlib import animation

import numpy as np
from scipy import integrate
from scipy import optimize

3.2. Bisection Method #

The Bisection method exploits the intermediate value theorem, where a continuous and differentiable function $f$ must have a zero between an interval $[a,b]$ such that $f(a)f(b)<0$, or equivalently, there must be a value $p\in[a,b]$ such that $f(p)=0$. Below the algorithmm is stated explicitly.

3.2.1. Steps BM#

There must be selected two values $a$ and $b$ such that $f(a)f(b)<0$ and $p\in[a,b]$ where $f(p)=0$. In other words, though we do not know the value of the root, we must know that there is at least one within the selected interval.
To begin, it must be set $a_1=a$ and $b_1=b$.
Calculate the mid-point $p_1$ as

\[p_1 = a_1 + \frac{b_1-a_1}{2} = \frac{a_1+b_1}{2}\]
Evaluate the function in $p_1$, if the stop condition is true, go to step 6.
If the stop condition is not satisfied, then:
1. If $f(p_1)f(a_1) > 0$, $p\in(p_1,b_1)$. Then set $a_2=p_1$ and $b_2=b_1$
2. If $f(p_1)f(a_1) < 0$, $p\in(a_1,p_1)$. Then set $a_2=a_1$ and $b_2=p_1$
3. Go to step 3 using $p_2$, $a_2$ and $b_2$ instead of $p_1$, $a_1$ and $b_1$. For next iterations the index increases until the stop condition is reached.
The End!

3.2.2. Stop condition BM#

There are several different stop conditions for this algorithm. The most used are stated below:

A fixed distance between the last two steps (absolute convergence): → xtol

\[|p_i - p_{i-1}|<\epsilon\]
A fixed relative distance between the last two steps (relative convergence): → rtol

\[\frac{|p_i - p_{i-1}|}{|p_i|}<\epsilon\ \ \ \ \ p_i \neq 0\]
Function tolerance:

\[f(p_i)< \epsilon\]

All these conditions should lead to a desired convergence expressed by the $\epsilon$ value. However, the first and the third conditions present some problems when the function has a derivative very large or close to $0$ as evaluated in the root value. When the function is very inclined, the first condition fails as a convergence in the $x$ axis does not guarantee a convergence in the $y$ axis, so the found root $p$ may be far from the real value. When the function is very flat ($dF/dx\rightarrow 0$), the third condition fails due to an analogous reason.

A final stop condition which does not have mathematical motivation but a computational one, is a maximum number of allowed iterations. This condition should be used not only for this algorithm but for all iteration-based numerical methods. This condition guarantees a finite computing time and prevents undesired infinite bucles.

If $N>N_{max}$, stop!

3.2.3. Error analysis BM#

If we suppose $f\in C[a,b]$ and $f(a)f(b)<0$, the Bisection method generates a sequence of numbers $\left\{p_i\right\}_{i=1}^\infty$ approximating a root $p$ of $f$ as:

\[|p_i-p|\leq \frac{b-a}{2^n},\ \ \ \ \ i\geq 1\]

From this, we can conclude the convergence rate of the method is

\[p_i = p + \mathcal{O}\left( \frac{1}{2^i} \right)\]

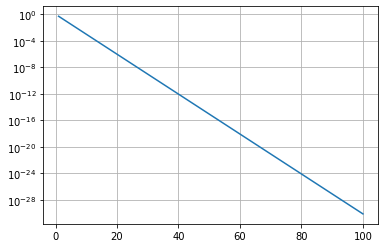
This expression allows us to estimate the maximum number of required iterations for achieving a desired precision. The next figure sketches the number of iterations required for some precision.

import time

i=np.arange( 1, 101)
i[:3]

array([1, 2, 3])

i[-1]

# 1/2**i → exp2(-i)
plt.semilogy(i,np.exp2(-i))
plt.grid()

../_images/one-variable-equations_21_0.png

s=time.time()
#Array of iterations
Niter = np.arange( 1, 100 )

plt.figure( figsize=(6,6) )
#plt.semilogy( Niter, 2.0**-Niter, color="green", lw = 2 )
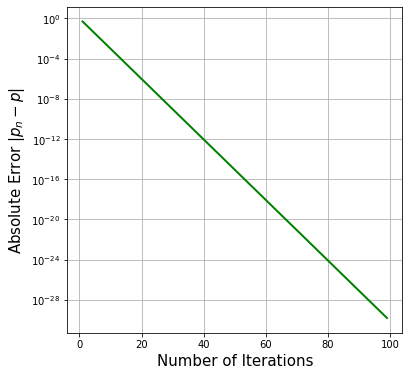
plt.semilogy( Niter, np.exp2(-Niter), color="green", lw = 2 )
plt.grid(True)
plt.xlabel("Number of Iterations",size=15)
plt.ylabel("Absolute Error $|p_n-p|$",size=15)
f=time.time()-s

../_images/one-variable-equations_22_0.png

3.2.4. Example 1#

Find the root of the function $f$

$f(x) = x^3 - 2$

for $20$ iterations, show the result and the relative error in each iteration.

2**(1/3)

1.2599210498948732

#Defining Bisection function
def Bisection( f, a, b, Nmax, printer=False ):
    """
    Find the root of function f between a and b
    
    f: function
    a,b: the initial interval
    Nmax: Nmax de interations
    printer: bool, to print internal steps
    """
    #verifying the STEP1, a and b with different signs
    if f(a)*f(b)>0:
        raise Exception("Error, f(a) and f(b) should have opposite signs")
    #Assigning the current extreme values, STEP2
    ai = a
    bi = b
    #Iterations
    n = 1
    while n<=Nmax:
        #Bisection, STEP3
        pi = (ai+bi)/2.0
        #Evaluating function in pi, STEP4 and STEP5
        if printer:
            print( f"Value for {n} iterations: {pi}" )
        #Condition A
        if f(pi)*f(ai)>0:
            ai = pi
        #Condition B
        else:
            bi = pi
        #Condition C: repeat the cycle
        n+=1
    #Final result
    return pi

Defining function

def function(x):
    return x**3.0 - 2.0

Finding the root of the function. The real root is $\sqrt[3]{2}$, so a and b should enclose this value

#Defining a and b
a = 0.0
b = 2.0
Nmax = 20
result = Bisection(function, a, b, Nmax, printer=True)
print ( "Real value:", 2**(1/3))
print ( "Absolute error", abs((2**(1/3)-result)) )

Value for 1 iterations: 1.0
Value for 2 iterations: 1.5
Value for 3 iterations: 1.25
Value for 4 iterations: 1.375
Value for 5 iterations: 1.3125
Value for 6 iterations: 1.28125
Value for 7 iterations: 1.265625
Value for 8 iterations: 1.2578125
Value for 9 iterations: 1.26171875
Value for 10 iterations: 1.259765625
Value for 11 iterations: 1.2607421875
Value for 12 iterations: 1.26025390625
Value for 13 iterations: 1.260009765625
Value for 14 iterations: 1.2598876953125
Value for 15 iterations: 1.25994873046875
Value for 16 iterations: 1.259918212890625
Value for 17 iterations: 1.2599334716796875
Value for 18 iterations: 1.2599258422851562
Value for 19 iterations: 1.2599220275878906
Value for 20 iterations: 1.2599201202392578
Real value: 1.2599210498948732
Absolute error 9.296556153781665e-07

Using the error analysis, we can predict the produced error at $20$ iterations by computing:

\[ \left( \frac{1}{2^{20}}\right) \approx 9.53674316\times 10^{-7} \]

This value is very close to the obtained relative error.

If we were interested in a double precision, i.e. $\epsilon \sim 10^{-17}$, the number of required iterations would be:

\[ 10^{-17} = \left( \frac{1}{2^{N}}\right) \longrightarrow N = \frac{17}{\log_{10}(2)} \approx 56 \]

Now the same but using scipy implementation

#Defining a and b
a = 0.0
b = 2.0
Nmax = 56
result = Bisection(function, a, b, Nmax, printer=True)
print ( "Real value:", 2**(1/3))
print ( "Absolute error", abs((2**(1/3)-result)) )

Value for 1 iterations: 1.0
Value for 2 iterations: 1.5
Value for 3 iterations: 1.25
Value for 4 iterations: 1.375
Value for 5 iterations: 1.3125
Value for 6 iterations: 1.28125
Value for 7 iterations: 1.265625
Value for 8 iterations: 1.2578125
Value for 9 iterations: 1.26171875
Value for 10 iterations: 1.259765625
Value for 11 iterations: 1.2607421875
Value for 12 iterations: 1.26025390625
Value for 13 iterations: 1.260009765625
Value for 14 iterations: 1.2598876953125
Value for 15 iterations: 1.25994873046875
Value for 16 iterations: 1.259918212890625
Value for 17 iterations: 1.2599334716796875
Value for 18 iterations: 1.2599258422851562
Value for 19 iterations: 1.2599220275878906
Value for 20 iterations: 1.2599201202392578
Value for 21 iterations: 1.2599210739135742
Value for 22 iterations: 1.259920597076416
Value for 23 iterations: 1.2599208354949951
Value for 24 iterations: 1.2599209547042847
Value for 25 iterations: 1.2599210143089294
Value for 26 iterations: 1.2599210441112518
Value for 27 iterations: 1.259921059012413
Value for 28 iterations: 1.2599210515618324
Value for 29 iterations: 1.2599210478365421
Value for 30 iterations: 1.2599210496991873
Value for 31 iterations: 1.2599210506305099
Value for 32 iterations: 1.2599210501648486
Value for 33 iterations: 1.259921049932018
Value for 34 iterations: 1.2599210498156026
Value for 35 iterations: 1.2599210498738103
Value for 36 iterations: 1.259921049902914
Value for 37 iterations: 1.2599210498883622
Value for 38 iterations: 1.2599210498956381
Value for 39 iterations: 1.2599210498920002
Value for 40 iterations: 1.2599210498938191
Value for 41 iterations: 1.2599210498947286
Value for 42 iterations: 1.2599210498951834
Value for 43 iterations: 1.259921049894956
Value for 44 iterations: 1.2599210498948423
Value for 45 iterations: 1.2599210498948992
Value for 46 iterations: 1.2599210498948707
Value for 47 iterations: 1.259921049894885
Value for 48 iterations: 1.2599210498948779
Value for 49 iterations: 1.2599210498948743
Value for 50 iterations: 1.2599210498948725
Value for 51 iterations: 1.2599210498948734
Value for 52 iterations: 1.259921049894873
Value for 53 iterations: 1.2599210498948732
Value for 54 iterations: 1.259921049894873
Value for 55 iterations: 1.259921049894873
Value for 56 iterations: 1.259921049894873
Real value: 1.2599210498948732
Absolute error 2.220446049250313e-16

from scipy import optimize

See help with optimize?:

Bisection?

Signature: Bisection(f, a, b, Nmax, printer=False)
Docstring:
Find the root of function f between a and b

f: function
a,b: the initial interval
Nmax: Nmax de interations
printer: bool, to print internal steps
File:      ~/ComputationalMethods/material/<ipython-input-17-364950e282c6>
Type:      function

optimize.bisect??

Signature:
optimize.bisect(
    f,
    a,
    b,
    args=(),
    xtol=2e-12,
    rtol=8.881784197001252e-16,
    maxiter=100,
    full_output=False,
    disp=True,
)
Source:   
def bisect(f, a, b, args=(),
           xtol=_xtol, rtol=_rtol, maxiter=_iter,
           full_output=False, disp=True):
    """
    Find root of a function within an interval using bisection.

    Basic bisection routine to find a zero of the function `f` between the
    arguments `a` and `b`. `f(a)` and `f(b)` cannot have the same signs.
    Slow but sure.

    Parameters
    ----------
    f : function
        Python function returning a number.  `f` must be continuous, and
        f(a) and f(b) must have opposite signs.
    a : scalar
        One end of the bracketing interval [a,b].
    b : scalar
        The other end of the bracketing interval [a,b].
    xtol : number, optional
        The computed root ``x0`` will satisfy ``np.allclose(x, x0,
        atol=xtol, rtol=rtol)``, where ``x`` is the exact root. The
        parameter must be nonnegative.
    rtol : number, optional
        The computed root ``x0`` will satisfy ``np.allclose(x, x0,
        atol=xtol, rtol=rtol)``, where ``x`` is the exact root. The
        parameter cannot be smaller than its default value of
        ``4*np.finfo(float).eps``.
    maxiter : int, optional
        if convergence is not achieved in `maxiter` iterations, an error is
        raised.  Must be >= 0.
    args : tuple, optional
        containing extra arguments for the function `f`.
        `f` is called by ``apply(f, (x)+args)``.
    full_output : bool, optional
        If `full_output` is False, the root is returned.  If `full_output` is
        True, the return value is ``(x, r)``, where x is the root, and r is
        a `RootResults` object.
    disp : bool, optional
        If True, raise RuntimeError if the algorithm didn't converge.
        Otherwise the convergence status is recorded in a `RootResults`
        return object.

    Returns
    -------
    x0 : float
        Zero of `f` between `a` and `b`.
    r : `RootResults` (present if ``full_output = True``)
        Object containing information about the convergence.  In particular,
        ``r.converged`` is True if the routine converged.

    Examples
    --------

    >>> def f(x):
    ...     return (x**2 - 1)

    >>> from scipy import optimize

    >>> root = optimize.bisect(f, 0, 2)
    >>> root
    1.0

    >>> root = optimize.bisect(f, -2, 0)
    >>> root
    -1.0

    See Also
    --------
    brentq, brenth, bisect, newton
    fixed_point : scalar fixed-point finder
    fsolve : n-dimensional root-finding

    """
    if not isinstance(args, tuple):
        args = (args,)
    if xtol <= 0:
        raise ValueError("xtol too small (%g <= 0)" % xtol)
    if rtol < _rtol:
        raise ValueError("rtol too small (%g < %g)" % (rtol, _rtol))
    r = _zeros._bisect(f, a, b, xtol, rtol, maxiter, args, full_output, disp)
    return results_c(full_output, r)
File:      /etc/anaconda3/lib/python3.6/site-packages/scipy/optimize/zeros.py
Type:      function

Check the help: See here

def f(x,n,c=2):
    return x**n-c

optimize.bisect(f,0,2,args=(3,)) 

1.2599210498938191

optimize.bisect(lambda x: f(x,3),0,2)

1.2599210498938191

help(optimize.bisect)

Help on function bisect in module scipy.optimize.zeros:

bisect(f, a, b, args=(), xtol=2e-12, rtol=8.881784197001252e-16, maxiter=100, full_output=False, disp=True)
    Find root of a function within an interval using bisection.
    
    Basic bisection routine to find a zero of the function `f` between the
    arguments `a` and `b`. `f(a)` and `f(b)` cannot have the same signs.
    Slow but sure.
    
    Parameters
    ----------
    f : function
        Python function returning a number.  `f` must be continuous, and
        f(a) and f(b) must have opposite signs.
    a : scalar
        One end of the bracketing interval [a,b].
    b : scalar
        The other end of the bracketing interval [a,b].
    xtol : number, optional
        The computed root ``x0`` will satisfy ``np.allclose(x, x0,
        atol=xtol, rtol=rtol)``, where ``x`` is the exact root. The
        parameter must be nonnegative.
    rtol : number, optional
        The computed root ``x0`` will satisfy ``np.allclose(x, x0,
        atol=xtol, rtol=rtol)``, where ``x`` is the exact root. The
        parameter cannot be smaller than its default value of
        ``4*np.finfo(float).eps``.
    maxiter : int, optional
        If convergence is not achieved in `maxiter` iterations, an error is
        raised. Must be >= 0.
    args : tuple, optional
        Containing extra arguments for the function `f`.
        `f` is called by ``apply(f, (x)+args)``.
    full_output : bool, optional
        If `full_output` is False, the root is returned. If `full_output` is
        True, the return value is ``(x, r)``, where x is the root, and r is
        a `RootResults` object.
    disp : bool, optional
        If True, raise RuntimeError if the algorithm didn't converge.
        Otherwise, the convergence status is recorded in a `RootResults`
        return object.
    
    Returns
    -------
    x0 : float
        Zero of `f` between `a` and `b`.
    r : `RootResults` (present if ``full_output = True``)
        Object containing information about the convergence. In particular,
        ``r.converged`` is True if the routine converged.
    
    Examples
    --------
    
    >>> def f(x):
    ...     return (x**2 - 1)
    
    >>> from scipy import optimize
    
    >>> root = optimize.bisect(f, 0, 2)
    >>> root
    1.0
    
    >>> root = optimize.bisect(f, -2, 0)
    >>> root
    -1.0
    
    See Also
    --------
    brentq, brenth, bisect, newton
    fixed_point : scalar fixed-point finder
    fsolve : n-dimensional root-finding

3.3. General arguments and options of a SciPy function #

Let define a general multiparameter

f with a mandatory parameter and two optional parameters, corresponding to a straight line with the slope and the intercept as parameters $$ f(x)=mx+b\,, $$

def f(x,m=3,b=-2):
    return m*x+b

f(0.66666666666666666,-3,2)

0.0

We have at least three ways to use a multiparameter function, the first two with the implicit lambda function

optimize.bisect(lambda x: -3*x+2,-10,10)

0.6666666666671972

optimize.bisect(lambda x: f(x,-3,2),-10,10,)

0.6666666666671972

and the recommended way to used the designed implementation in Scipy through the args parameter which is common to many methods

optimize.bisect(f,-10,10,args=(-3,2))

0.6666666666671972

xtol

optimize.bisect(f,-10,10,args=(-3,2),xtol=1E-17)

0.6666666666666671

maxiter

optimize.bisect(f,-10,10,args=(-3,2),xtol=1E-17,maxiter=10000)

0.6666666666666671

optimize.bisect(f,-10,10,args=(-3,2),xtol=1E-17,rtol=1E-15,maxiter=10000)

0.6666666666666671

full_output

x0,r=optimize.bisect(f,-10,10,args=(-3,2),xtol=1E-17,full_output=True)

x0

0.6666666666666671

type(r)

scipy.optimize.zeros.RootResults

Check the code

r.root

0.6666666666666671

The help of the function is write directly in the code of the Scipy method bisect

optimize.bisect??

Check the internal referenced code

optimize._zeros??

Type:        module
String form: <module 'scipy.optimize._zeros' from '/usr/local/lib/python3.7/dist-packages/scipy/optimize/_zeros.cpython-37m-x86_64-linux-gnu.so'>
File:        /usr/local/lib/python3.7/dist-packages/scipy/optimize/_zeros.cpython-37m-x86_64-linux-gnu.so

3.3.1. Example#

Find the roots of $$x^3=2$$

def function(x):
    return x**3.0 - 2.0

todo=optimize.bisect(function,a,b,full_output=True)

type(todo)

tuple

len(todo)

result=todo[0]
result

1.2599210498938191

r=todo[1]
r

      converged: True
           flag: 'converged'
 function_calls: 42
     iterations: 40
           root: 1.2599210498938191

type(r)

scipy.optimize.zeros.RootResults

r.iterations

todo=optimize.bisect(function,a,b,full_output=False)

type(todo)

float

a = 0.0
b = 2.0

result,r=optimize.bisect(function,a,b,full_output=True)

result

1.2599210498938191

2**(1/3.0)

1.2599210498948732

Check r object by using the <TAB> key next

r.iterations

r.function_calls

2**(-r.iterations)

9.094947017729282e-13

abs((2**(1/3.0)-result))

1.0540457395791236e-12

r.converged

True

result,r=optimize.bisect(function,a,b,xtol=1E-17,full_output=True)

r.iterations

abs((2**(1/3.0)-result))

2.220446049250313e-16

2**(-r.iterations)

4.440892098500626e-16

ACTIVITY

In an IPython notebook, use the scipy implementation and find the first solution to the equation

$ 7 = \sqrt{x^2+1}+e^x\sin x $

CLUE: Check graphically (with matplotlib) that the solution is within the interval $[0,2]$.

solution

a,b,c=(2,3,4)

import numpy as np

# Solo usar para constante
np.e

2.718281828459045

np.exp(1)

2.718281828459045

3.3.2. Example 2#

In orbital mechanics, when solving the central-force problem it becomes necessary to solve the Kepler’s equation. This is a transcendental equation that relates the orbital parameters of the trajectory.

Kepler equation: $M = E - \epsilon \sin E$

where $M$ is the mean anomaly, $E$ the eccentric anomaly and $\epsilon$ the eccentricity. The mean anomaly can be computed with the expression

\[M = n\ t = \sqrt{ \frac{GM}{a^3} } t\]

where $n$ is the mean motion, $G$ the gravitational constant, $M$ the mass of the central body and $a$ the semi-major axis. $t$ is the time where the position in the trajectory will be computed.

The coordinates $x$ and $y$ as time functions can be recovered by means of the next expressions

\[x(t) = a(\cos E - \epsilon)\]

\[y(t) = b\sin E\]

where $b = a \sqrt{1-\epsilon^2}$ is the semi-minor axis of the orbit and the implicit time-dependence of the eccentric anomaly $E$ is computed through the Kepler’s equation.

Problem:

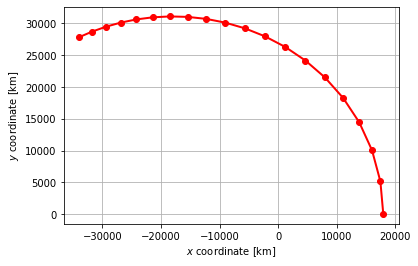
For a stallite orbiting the earth in a equatorial trajectory with eccentricity $\epsilon = 0.5$ at a geostationary distance for the semi-major axis, tabulate the positions $x$ and $y$ within the orbital plane in intervals of $15$ min during $5$ hours.

Parameters:

$\epsilon = 0.5$
$a = 35900$ km
$G = 6.67384 \times 10^{-11}$ m$^3$ kg$^{-1}$ s$^{-2}$
$M_{\oplus} = 5.972\times 10^{24}$ kg

#====================================================================
#Parameters
#====================================================================
#Eccentricity
eps = 0.5
#Semi-major axis    [m]
a = 35900e3
#Gravitational constant    [m3kg-1s-2]
GC = 6.67384e-11
#Earth mass    [kg]
Me = 5.972e24

#Semi-minor axis    [m]
b = a*(1-eps**2.0)**0.5
#Mean motion
n = ( GC*Me/a**3.0 )**0.5

#Hour to Second
HR2SC = 3600.
#Initial time    [hr]
t0 = 0*HR2SC
#Final time    [hr]
tf = 5*HR2SC
#Time step    [hr]
tstep = 0.25*HR2SC
#Number of maxim iterations
Niter = 56
#Root interval
a0 = -10
b0 = 10

#====================================================================
#Kepler Function
#====================================================================
def kepler( E ):
    func = E - eps*np.sin(E) - n*t
    return func

#====================================================================
#Position function
#====================================================================
def r(E):
    x = a*(np.cos(E)-eps)
    y = b*np.sin(E)
    return [x/1.e3, y/1.e3]

#====================================================================
#Solving for different times
#====================================================================
#Time array
times = np.arange( t0, tf, tstep )

rpos = []
for t in times:
    #Finding the new eccentric anomaly
    E = optimize.bisect( kepler, a0, b0 )
    #Computing coordinates at this time
    ri = r(E)
    print ("In %f hours, the satellite is located at (%f,%f) km"%(t/HR2SC, ri[0], ri[1]) )
    rpos.append( ri )
rpos = np.array(rpos)    

#Plotting
plt.plot( rpos[:,0], rpos[:,1], "o-", color="red", lw = 2 )
plt.grid(True)
plt.xlabel("$x$ coordinate [km]")
plt.ylabel("$y$ coordinate [km]")

In 0.000000 hours, the satellite is located at (17950.000000,0.000000) km
In 0.250000 hours, the satellite is located at (17454.741542,5146.426647) km
In 0.500000 hours, the satellite is located at (16033.097675,10023.437750) km
In 0.750000 hours, the satellite is located at (13848.847528,14430.262364) km
In 1.000000 hours, the satellite is located at (11104.379909,18261.701894) km
In 1.250000 hours, the satellite is located at (7989.437466,21493.410338) km
In 1.500000 hours, the satellite is located at (4657.168469,24151.489610) km
In 1.750000 hours, the satellite is located at (1221.066166,26286.121177) km
In 2.000000 hours, the satellite is located at (-2238.747501,27954.872718) km
In 2.250000 hours, the satellite is located at (-5667.264143,29214.008624) km
In 2.500000 hours, the satellite is located at (-9027.373695,30114.739827) km
In 2.750000 hours, the satellite is located at (-12294.392344,30702.085866) km
In 3.000000 hours, the satellite is located at (-15452.164136,31014.965936) km
In 3.250000 hours, the satellite is located at (-18490.361033,31086.789919) km
In 3.500000 hours, the satellite is located at (-21402.633716,30946.195086) km
In 3.750000 hours, the satellite is located at (-24185.347784,30617.769816) km
In 4.000000 hours, the satellite is located at (-26836.717825,30122.702148) km
In 4.250000 hours, the satellite is located at (-29356.211228,29479.336137) km
In 4.500000 hours, the satellite is located at (-31744.135350,28703.638662) km
In 4.750000 hours, the satellite is located at (-34001.350021,27809.586870) km

Text(0, 0.5, '$y$ coordinate [km]')

../_images/one-variable-equations_103_2.png

Created in Deepnote

Computational Methods

One Variable Equations