Matplotlib #

Matplotlib is a python 2D plotting library which produces publication quality figures in a variety of hardcopy formats and interactive environments across platforms. matplotlib can be used in python scripts, the python and ipython shell, web application servers, and six graphical user interface toolkits.

Matplotlib tries to make easy things easy and hard things possible. You can generate plots, histograms, power spectra, bar charts, errorcharts, scatterplots, etc, with just a few lines of code. For a sampling, see the screenshots, thumbnail gallery, and examples directory

For simple plotting the pyplot interface provides a MATLAB-like interface, particularly when combined with IPython. For the power user, you have full control of line styles, font properties, axes properties, etc, via an object oriented interface or via a set of functions familiar to MATLAB users.

Official page

Contents

Matplotlib
Basic Use
Gallery

Basic Use #

One of the most appealing advantages of Matplotlib is its versatility. You can use it in a very basic way as well as in a very customizable way, allowing a total control of what we want to sketch. We illustrate here some of the basic functions.

#Importing numpy
import numpy as np
#Ignore me!! (for scripts)
%pylab inline
#Importing matplotlib
import matplotlib.pyplot as plt

Populating the interactive namespace from numpy and matplotlib

%pylab inline

Populating the interactive namespace from numpy and matplotlib

The line %pylab inline is always necessary when using a IPython notebook. If you are working on the interpreter or with scripts, always use the function plt.show() in order to display the resulting image.

#Ploting a function
x = np.linspace( 0, 2*np.pi, 500 )
y = np.sin( x )
plt.plot( x, y )
#plt.plot( x, y,'.' )

[<matplotlib.lines.Line2D at 0x7f35a49404e0>]

#Scatter of points
X = np.random.random(200)
Y = np.random.random(200)
plt.plot( X, Y,'ro')

[<matplotlib.lines.Line2D at 0x7f35a4899400>]

#Multiple plots
#Ploting a function
x = np.linspace( 0, 2*np.pi, 100 )
plt.plot( x, np.sin( x ) )
plt.plot( x, np.cos( x ) )

[<matplotlib.lines.Line2D at 0x7f35a404c898>]

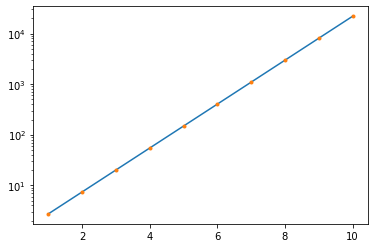
#Logaritmic axis Y
x = np.linspace( 1, 10, 10 )
plt.semilogy( x, np.exp( x ) )
p=plt.semilogy( x, np.exp( x ),'.' )

p[0]

<matplotlib.lines.Line2D at 0x7f359ee7c908>

array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

np.exp(x)

array([2.71828183e+00, 7.38905610e+00, 2.00855369e+01, 5.45981500e+01,
       1.48413159e+02, 4.03428793e+02, 1.09663316e+03, 2.98095799e+03,
       8.10308393e+03, 2.20264658e+04])

#Logaritmic axis X
x = np.linspace( 1, 10, 100 )
plt.semilogx( x, np.log( x ) )

[<matplotlib.lines.Line2D at 0x7f359ec94518>]

#Double Logaritmic axis
x = np.linspace( 0.1, 16.5*np.pi, 200 )
plt.loglog( x, np.sin( x )**2 )
plt.loglog( x, np.sin( x )**2,'.' )

[<matplotlib.lines.Line2D at 0x7f359ec514a8>]

#Double Logaritmic axis
x = np.logspace( np.log10(0.1), np.log10(16.5*np.pi), 200 )
plt.loglog( x, np.sin( x )**2 )
plt.loglog( x, np.sin( x )**2,'.' )

[<matplotlib.lines.Line2D at 0x7ffb7c296978>]

#Polar plots
r = np.arange( 0, 3.0, 0.01 )
theta = 2*np.pi*r

plt.subplot(111, polar=True)
plt.plot( theta, r )

[<matplotlib.lines.Line2D at 0x7f359ef9dda0>]

#Fill between
x = np.arange( 0, 2, 0.1 )
y1 = x/2.
y2 = x**2 + 1
plt.fill_between( x, y1, y2,alpha=0.6 )

<matplotlib.collections.PolyCollection at 0x7f359ef43b00>

#Multiple figures
X = np.arange( 0, 10, 0.1 )
#First plot
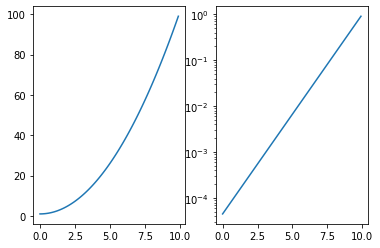
plt.subplot( 1, 2, 1 )
plt.plot( X, X**2+1 )
#Second plot
plt.subplot( 1, 2, 2 )
plt.semilogy( X, np.exp(X-10) )

[<matplotlib.lines.Line2D at 0x7f359eb243c8>]

#Histograms
X = np.random.random( 500 )
plt.hist( X )

(array([54., 54., 48., 53., 40., 53., 47., 46., 51., 54.]),
 array([0.0026303 , 0.10221054, 0.20179078, 0.30137101, 0.40095125,
        0.50053148, 0.60011172, 0.69969195, 0.79927219, 0.89885243,
        0.99843266]),
 <BarContainer object of 10 artists>)

Animmations #

See: http://louistiao.me/posts/notebooks/embedding-matplotlib-animations-in-jupyter-as-interactive-javascript-widgets/

import matplotlib.pyplot as plt
import matplotlib.animation
import numpy as np

t = np.linspace(0,2*np.pi)
x = np.sin(t)

fig, ax = plt.subplots()
ax.axis([0,2*np.pi,-1,1])
l, = ax.plot([],[])

def animate(i):
    l.set_data(t[:i], x[:i])

#Avoid intial plot
plt.close()
ani = matplotlib.animation.FuncAnimation(fig, animate, frames=len(t))

from IPython.display import HTML
HTML(ani.to_jshtml())

Easy animmations with video output #

#See 
from IPython.display import HTML
from matplotlib import pyplot as plt
from celluloid import Camera

plt.ioff()
fig = plt.figure()
camera = Camera(fig)
for i in range(10):
    plt.plot([i] * 10)
    camera.snap()
plt.close()
animation = camera.animate()
animation.save('animation.mp4')
HTML(animation.to_html5_video())

The double pendulum problem #

(No usar cómo trabajo final)

From https://matplotlib.org/stable/gallery/animation/double_pendulum.html

from numpy import sin, cos
import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as integrate
import matplotlib.animation as animation
from collections import deque

G = 9.8  # acceleration due to gravity, in m/s^2
L1 = 1.0  # length of pendulum 1 in m
L2 = 1.0  # length of pendulum 2 in m
L = L1 + L2  # maximal length of the combined pendulum
M1 = 1.0  # mass of pendulum 1 in kg
M2 = 1.0  # mass of pendulum 2 in kg
t_stop = 5  # how many seconds to simulate
history_len = 500  # how many trajectory points to display


def derivs(state, t):

    dydx = np.zeros_like(state)
    dydx[0] = state[1]

    delta = state[2] - state[0]
    den1 = (M1+M2) * L1 - M2 * L1 * cos(delta) * cos(delta)
    dydx[1] = ((M2 * L1 * state[1] * state[1] * sin(delta) * cos(delta)
                + M2 * G * sin(state[2]) * cos(delta)
                + M2 * L2 * state[3] * state[3] * sin(delta)
                - (M1+M2) * G * sin(state[0]))
               / den1)

    dydx[2] = state[3]

    den2 = (L2/L1) * den1
    dydx[3] = ((- M2 * L2 * state[3] * state[3] * sin(delta) * cos(delta)
                + (M1+M2) * G * sin(state[0]) * cos(delta)
                - (M1+M2) * L1 * state[1] * state[1] * sin(delta)
                - (M1+M2) * G * sin(state[2]))
               / den2)

    return dydx

# create a time array from 0..t_stop sampled at 0.02 second steps
dt = 0.02
t = np.arange(0, t_stop, dt)

# th1 and th2 are the initial angles (degrees)
# w10 and w20 are the initial angular velocities (degrees per second)
th1 = 120.0
w1 = 0.0
th2 = -10.0
w2 = 0.0

# initial state
state = np.radians([th1, w1, th2, w2])

# integrate your ODE using scipy.integrate.
y = integrate.odeint(derivs, state, t)

x1 = L1*sin(y[:, 0])
y1 = -L1*cos(y[:, 0])

x2 = L2*sin(y[:, 2]) + x1
y2 = -L2*cos(y[:, 2]) + y1

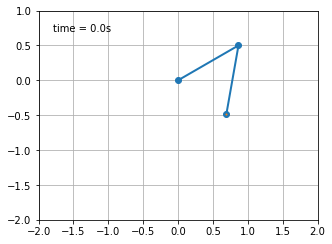
fig = plt.figure(figsize=(5, 4))
ax = fig.add_subplot(autoscale_on=False, xlim=(-L, L), ylim=(-L, 1.))
ax.set_aspect('equal')
ax.grid()

line, = ax.plot([], [], 'o-', lw=2)
trace, = ax.plot([], [], '.-', lw=1, ms=2)
time_template = 'time = %.1fs'
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
history_x, history_y = deque(maxlen=history_len), deque(maxlen=history_len)


def animate(i):
    thisx = [0, x1[i], x2[i]]
    thisy = [0, y1[i], y2[i]]

    if i == 0:
        history_x.clear()
        history_y.clear()

    history_x.appendleft(thisx[2])
    history_y.appendleft(thisy[2])

    line.set_data(thisx, thisy)
    trace.set_data(history_x, history_y)
    time_text.set_text(time_template % (i*dt))
    return line, trace, time_text


ani = animation.FuncAnimation(
    fig, animate, len(y), interval=dt*1000, blit=True)
plt.show()

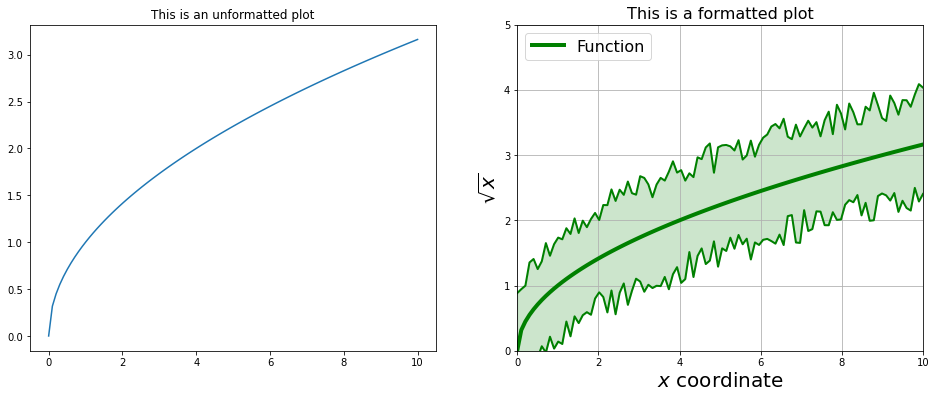
Formating Figures #

Matplotlib supports complex formatting, even allowing LaTeX expressions. These features makes Matplotlib a very appealing package for making professional figures, for example for a scientific paper. Next it is shown an example (script) where you can see some of the capabilities of Matplotlib

#! /usr/bin/python
#====================================================================
#Importing libraries
#====================================================================
import numpy as np
import matplotlib.pyplot as plt

#Arrays
X = np.linspace( 0, 10, 100 )
Y = X**0.5
Y1 = Y+0.5*(1+np.random.random(100))
Y2 = Y-0.5*(1+np.random.random(100))

#Setting the figure environment
plt.figure( figsize = (16,6) )

#====================================================================
#First plot
#====================================================================
plt.subplot( 1, 2, 1 )
plt.plot( X, Y )
plt.title( "This is an unformatted plot" )

#====================================================================
#Second plot
#====================================================================
plt.subplot( 1, 2, 2 )
#2D Plots
plt.plot( X, Y, linewidth=4, color="green", label="Function" )
plt.plot( X, Y1, linewidth=2, color="green" )
plt.plot( X, Y2, linewidth=2, color="green" )
#Error region
plt.fill_between( X, Y1, Y2, color="green", alpha=0.2 )
#Grid
plt.grid( True )
#X-axis limits
plt.xlim( (0, 10) )
#Y-axis limits
plt.ylim( (0, 5) )
#Label
plt.legend( loc="upper left", fontsize=16 )
#X label
plt.xlabel( "$x$ coordinate", fontsize=20 )
#Y label
plt.ylabel( "$\sqrt{x}$", fontsize=20 )
#Title
plt.title( "This is a formatted plot", fontsize=16 )

#====================================================================
#Showing
#====================================================================
#You can store this figure in any format, even in vectorial formats 
#like pdf
plt.savefig( "Figure.pdf" )
#Showing the figure on screen
plt.show()

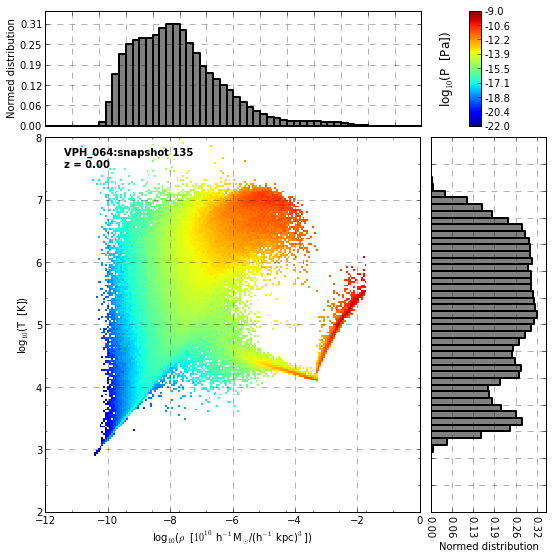
Gallery #

This gallery comprehends some interesting advanced uses of matplotlib.

from IPython.core.display import Image 
Image(filename='./figures/voids.png')

Image(filename='./figures/VPHphase.png')

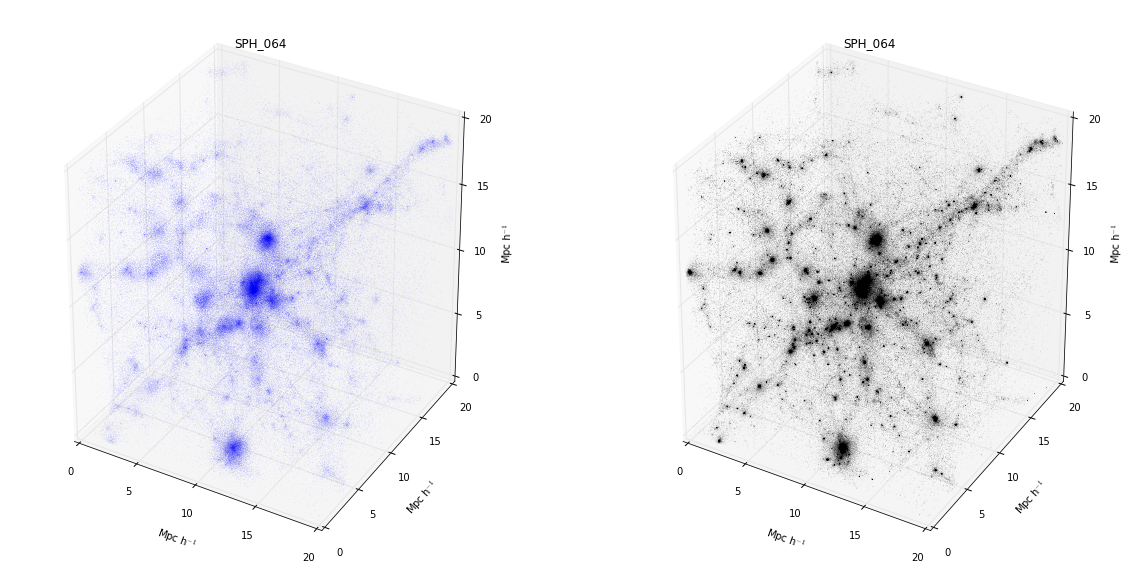
Image(filename='./figures/simulation.png')

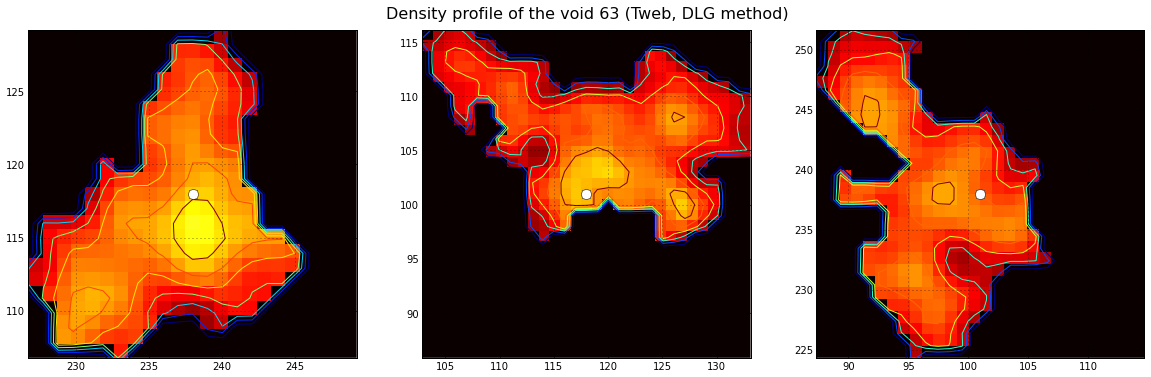
Image(filename='./figures/voiddensity.png')

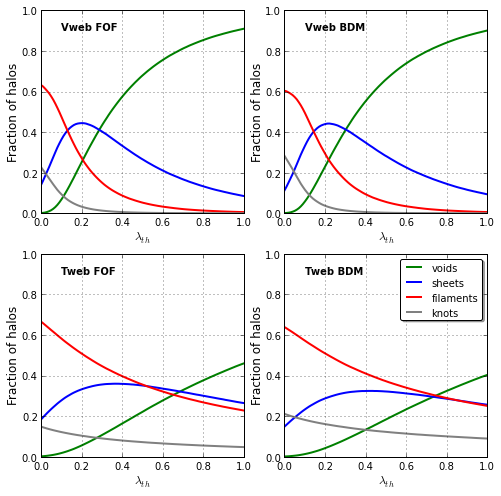
Image(filename='./figures/halosfraction.png')

The orbit of a point $P$ is defined by the following parametric equation for $-2 \cdot \pi<t<2 \cdot \pi$. $$ \left\{\begin{array}{l} x(t)=\cos (t)+\cos \left(\frac{1}{2} \cdot t\right), \\ y(t)=\sin (t)+\sin \left(\frac{1}{2} \cdot t\right) \end{array}\right. $$ The point $P$ passes through the $x$-axis in the origin. It passes through $x$-axis two more times. Determine the values of $t$ where this happens. Give your answer as a list $[\square, \square]$.

%pylab inline

Populating the interactive namespace from numpy and matplotlib

import numpy as np
import pandas as pd

π=np.pi

t=np.linspace(-2*π,2*π,100)

plt.plot(np.cos(t)+np.cos(t/2), np.sin(t)+np.sin(t/2))
plt.grid()
θ=-2*π
plt.plot(np.cos(θ)+np.cos(θ/2), np.sin(θ)+np.sin(θ/2),'bo')
θ=0
plt.plot(np.cos(θ)+np.cos(θ/2), np.sin(θ)+np.sin(θ/2),'ko')
θ=4*π/3
plt.plot(np.cos(θ)+np.cos(θ/2), np.sin(θ)+np.sin(θ/2),'ro')

[<matplotlib.lines.Line2D at 0x7faf830905e0>]

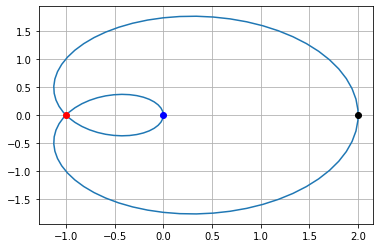
([2,0],[-1,0])

([2, 0], [-1, 0])

Computational Methods

Matplotlib

Contents

Matplotlib#

Basic Use#

Animmations#

Easy animmations with video output#

The double pendulum problem#

Formating Figures#

Gallery#