2. Computer Arithmetics and Round-off Methods#

Actividades: https://classroom.github.com/a/2v-HnNqn

In a symbolic computation programs, implemented in SymPy or Mathematica for example, operatios like $1/3+4/3=5/3$, $2\times 3/4 = 3/2$, $(\sqrt{2})^2 = 2$ are unambiguously defined, However, when one numerical programming languages are used to represent numbers in a computer, this is no longer true. The main reason of this is the so-called finite arithmetic, what is the way in which a numerical computer programs performs basic operations. Some features of finite arithmetic are stated below:

Only integer and rational numbers can be exactly represented.
The elements of the set in which arithmetic is performed is necessarily finite.
Any arithmetic operation between two or more numbers of this set should be another element of the set.
Non-representable numbers like irrational numbers are approximated to the closest rational number within the defined set.
Extremely large numbers produce overflows and extremely small numbers produce underflows, which are taken as null.
Operations over non-representable numbers are not exact.

In spite of this, defining adequately the set of elements in which our computer will operate, round-off methods can be systematically neglected, yielding correct results within reasonable error margins. In some pathological cases, when massive iterations are required, these errors must be taken into account more seriously.

Binary machine numbers
- Single-precision numbers
- Double-precision numbers
Finite Arithmetic
- Addition
- Multiplication

2.1. More About Float Values#

2.2. Binary machine numbers#

We will obtain the general algorithm to obtain the binary r

2.2.1. Integers#

From here: If you recall your mathematics, then it will be easy for you to find out how we turn an integer number to its binary representation. Let’s take for example the number 47. (see ‘//’ operator here)

We divide 47 by 2. The quotient is int(47//2) → 23 and the remainder is 47%2 → 1
We divide the quotient of the previous step by 2. The new quotient is int(23//2) → 11 and the remainder is 23%2 → 1.
We divide the quotient of the previous step by 2. The new quotient is int(11/2) → 5 and the remainder is 11%2 → 1.
We divide the quotient of the previous step by 2. The new quotient is int(5//2) → 2 and the remainder is 5%2 → 1.
We divide the quotient of the previous step by 2. The new quotient is int(2//2) → 1 and the remainder is 2%2 → 0.
We divide the quotient of the previous step by 2. The new quotient is int(1//2) → 0 and the remainder is 1%2 → 1
We stop here, when the last quotient is 1//2→0.

Then, the binary representation is the series of __1__s and __0__s of the remainders, taken in reverse order to the one produced, from latest to earliest: 101111.

Activity: Implement a function that get the binary representation of an integer.

x=47
b=''
while x!=0:
    oldx=x
    b=str(x%2)+b
    x=x//2
    print(f'x={oldx}/2={x} → b={b}')

x=47/2=23 → b=1
x=23/2=11 → b=11
x=11/2=5 → b=111
x=5/2=2 → b=1111
x=2/2=1 → b=01111
x=1/2=0 → b=101111

Activity: Return as a string with 8 charactes completed with leading zeroes. Use the string method: .rjust(8,"0")

b=b.rjust(8,'0')
print(f'b={b}')

b=00101111

Activity Write your function in the following format

#!/usr/bin/env python3
def mybin(x):
    print('__name__ = {}'.format(__name__))
    #Write your code here and change the next line as required
    return bin(x)[2:].rjust(8, "0")
if __name__=='__main__':
    n=input('Escriba un entero:\n')
    b=mybin(int(n))
    print('Su representación binaria es: {}'.format(b))

Overwriting mybin.py

The advantage of this standard format is that can be used directly as a python module, because in that case the variable __name__ evaluates to the name of the function. To check this, we first use a cell of the notebook just as a editor with the Jupyter magic function %%writefile

%%writefile mybin.py
#!/usr/bin/env python3
def mybin(x):
    print('__name__ = {}'.format(__name__))
    return bin(x)[2:].rjust(8, "0")
if __name__=='__main__':
    n=input('Escriba un entero;\n')
    b=mybin(int(n))
    print('Su representación binaria es: {}'.format(b))

Overwriting mybin.py

We now can use the full contents of the file as an usual python module, it it is in the working directory

import mybin as my
my.mybin(45)

__name__ = mybin

'00101101'

while here, or in a terminal:

__name__

'__main__'

Check with bin

The binary representation of a float in 32 bits done by the following steps

bin(47)

'0b101111'

The format is not the standard one. We need drop the first ‘0b’

bin(47)[2:]

'101111'

We must enforce the 8 bits representation by padding any additional leading zeroes

bin(47)[2:].rjust(8, '0')

'00101111'

To convert a binary into the integer we can use the int function with base=0 upont the proper Python formatted string, starting with: 0b

int('0b101111',base=0)

or with any number of padding zeroes in between

int('0b0000000101111',base=0)

It is rather straightforward to check that the binary representation is consistent:

0	0	1	0	1	1	1	1	Total
128	64	32	16	8	4	2	1
0	0	32	0	8	4	2	1	47

2.2.2. Floats#

Floats in 32 bits are representated trough 4 8-bit integers.

The processes of obtain the binary representation for a float can be complicated because the design used to really store the number in one specific programming language like Python. In fact, from https://stackoverflow.com/a/16444778/2268280:

To obtain the four integers associated to a real number we need first to ask for the packed structure : '!', in 32 bits: 'f', with the full string '!f' as

import struct
packed=struct.pack('!f',0.15625)
packed

b'> \x00\x00'

type(packed)

bytes

This is a packed Python list with the four integers inside

[n for n in packed]

[62, 32, 0, 0]

Using the previous function to convert into a list of 8-bit strings

lb=[ mybin(n) for n in packed]
lb

__name__ = __main__
__name__ = __main__
__name__ = __main__
__name__ = __main__

['00111110', '00100000', '00000000', '00000000']

The float representation is just the string formed with the four binaries

''.join(lb)

'00111110001000000000000000000000'

2.2.2.1. Full implementation#

import struct

def binary(num):
#num=3
#if True:
    # Struct can provide us with the float packed into bytes. The '!' ensures that
    # it's in network byte order (big-endian) and the 'f' says that it should be
    # packed as a float: 32 bites. Alternatively, for double-precision, you could use 'd'.
    packed = struct.pack('!f', num)
    print( 'Packed: %s' % repr(packed))

    # For each character in the returned string, we'll turn it into its corresponding
    # integer code point
    # 
    integers = [c for c in packed]
    print( 'Integers: %s' % integers)

    # For each integer, we'll convert it to its binary representation.
    binaries = [bin(i) for i in integers]
    print( 'Binaries: %s' % binaries)

    # Now strip off the '0b' from each of these
    stripped_binaries = [s.replace('0b', '') for s in binaries]
    print( 'Stripped: %s' % stripped_binaries)

    # Pad each byte's binary representation's with 0's to make sure it has all 8 bits:
    #
    # ['00111110', '10100011', '11010111', '00001010']
    padded = [s.rjust(8, '0') for s in stripped_binaries]
    print( 'Padded: %s' % padded)

    # At this point, we have each of the bytes for the network byte ordered float
    # in an array as binary strings. Now we just concatenate them to get the total
    # representation of the float:
    return ''.join(padded)

BIN=binary(0.15625)
BIN

Packed: b'> \x00\x00'
Integers: [62, 32, 0, 0]
Binaries: ['0b111110', '0b100000', '0b0', '0b0']
Stripped: ['111110', '100000', '0', '0']
Padded: ['00111110', '00100000', '00000000', '00000000']

'00111110001000000000000000000000'

''.join( list(BIN)[::-1] ) #inverted list joined into a string

'00000000000000000000010001111100'

2.2.3. Binary machine numbers#

As everyone knows, the base of the modern computation is the binary numbers. The binary base or base-2 numeral system is the simplest one among the existing numeral bases. As every electronic devices are based on logic circuits (circuits operating with logic gates), the implementation of a binary base is straightforward, besides, any other numeral system can be reduced to a binary representation.

According to the standard IEEE 754-2008, representation of real numbers can be done in several ways, single-precision and double precision are the most used ones.

2.2.3.1. Single-precision numbers#

Single-precision numbers are used when one does not need very accurate results and/or need to save memory. These numbers are represented by a 32-bits (Binary digIT) lenght binary number, where the real number is stored following the next rules:

The last 23 bits represent the fractional part of the number, b_i, with i=0,...22
The next 8 bits represent the exponent of the number, e, given by $$e = \sum_{i=0}^7 b_{23+i}2^i$$
The fist digit (called s) indicates the sign of the number (s=0 means a positive number, s=1 a negative one).

The formula for recovering the real number is then given by:

\[r = \frac{(-1)^s}{2^{127-e}} \left( 1 + \sum_{i=0}^{22}\frac{b_{i}}{2^{23-i}} \right)\]

where $s$ is the sign, $b_{23-i}$ the fraction bits and $e$ is given by:

Next, it is shown a little routine for calculating the value of the represented 32-bits number

2.2.4. ACTIVITY#

With the binary representation please try to implement the formula to recover the number.

Hint: Use as input the binary representation as a string and invert its order

SOLUTION:

The goal of this course is try to implement all the algorithms in terms of array operations, instead of use the loops of Pyhton like the for loop.

In this way, we need to interpret the formula in terms of arrays operations. If we manage to achieve that, then NumPy will be take care of the internal loops, which are much faster than the Python loops. As a bonus, the code is more compact and readable.

For example:

(2.1)#\[\begin{align} \sum_{i=0}^{22}\frac{b_{i}}{2^{23-i}}=&\frac{b[0]}{2^{23}}+\frac{b[1]}{2^{22}} +\cdots +\frac{b[21]}{2^2}+\frac{b[22]}{2^1}\nonumber\\ =&\frac{b[0:23]}{2^{[23,22,...,1]}}.\operatorname{sum()}\nonumber\\ =&\frac{b[0:23]}{2^{[1,2,...,23][::-1]}}.\operatorname{sum()} \end{align}\]

To implement the full formula: $$r = \frac{(-1)^s}{2^{127-e}} \left( 1 + \sum_{i=0}^{22}\frac{b_{i}}{2^{23-i}} \right)$$ with $$e = \sum_{i=0}^7 b_{23+i}2^i$$

e=(b[23:30]*2**(np.arange(8))).sum()

import numpy as np
def number32(BIN):
#if True:
    #BIN='00111110001000000000000000000000'
    #Inverting binary string
    b_inverted=np.array(list(BIN)[::-1]).astype(int)
    
    s=b_inverted[31]
    #Exponent part
    be=b_inverted[23:31]
    i=np.arange(be.size)
    e=(be*(2**i)).sum()
    
    bf=b_inverted[0:23]
    i_inverted=np.arange(1,bf.size+1)[::-1]

    numero=( (-1)**s/2**(127-e)  )*( 1 + (bf/2**i_inverted).sum() ) 
    return numero

print(number32('00111110001000000000000000000000'))

0.15625

Check aginst the implementation with for’s

## %load numtobin.py
def num32( binary ):
    #Inverting binary string
    binary = binary[::-1]
    s=binary[31]
    #Decimal part
    dec = 1
    for i in range(1,24):
        dec += int(binary[23-i])*2**-i
    #Exponent part
    exp = 0
    for i in range(0,8):
        exp += int(binary[23+i])*2**i
    #Total number
    number =( (-1)**int(s)/2**(127-exp) )*dec
    return number

print(num32('00111110001000000000000000000000'))

0.15625

Single-precision system can represent real numbers within the interval $\pm 10^{-38} \cdots 10^{38}$, with $7-8$ decimal digits.

#Decimal digits 
print("\n")
print( "Decimal digits contributions for single precision number")
print( 2**-23., 2**-15., 2**-5. , "\n")

#Largest and smallest exponent  
emax = 0 
for i in range(0,8):
    emax += 2**i
print( "Largest and smallest exponent for single precision number" )
print( 2**(emax-127.), 2**(-127.),"\n" )

Decimal digits contributions for single precision number
1.1920928955078125e-07 3.0517578125e-05 0.03125 

Largest and smallest exponent for single precision number
3.402823669209385e+38 5.877471754111438e-39 

2.2.4.1. Double-precision numbers#

Double-precision numbers are used when high accuracy is required. These numbers are represented by a 64-bits (Binary digIT) lenght binary number, where the real number is stored following the next rules:

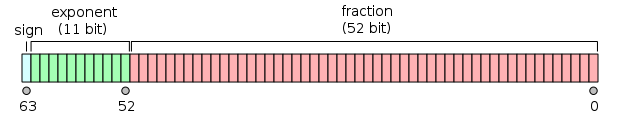
The fist digit (called s) indicates the sign of the number (s=0 means a positive number, s=1 a negative one).
The next 11 bits represent the exponent of the number.
The last bits represent the fractional part of the number.

The formula for recovering the real number is then given by:

\[r = (-1)^s\times \left( 1 + \sum_{i=1}^{52}b_{52-i}2^{-i} \right)\times 2^{e-1023}\]

where $s$ is the sign, $b_{23-i}$ the fraction bits and $e$ is given by:

\[e = \sum_{i=0}^{10} b_{52+i}2^i\]

Double-precision system can represent real numbers within the interval $\pm 10^{-308} \cdots 10^{308}$, with $16-17$ decimal digits.

1e307 * 10

1e+308

1e307 * 20

inf

1e-323

1e-323

1e-324

0.0

2.2.5. ACTIVITY#

1. Write a python script that calculates the double precision number represented by a 64-bits binary.

2. What is the number represented by:

0 10000000011 1011100100001111111111111111111111111111111111111111

**ANSWER:** 27.56640625

2.3. Finite Arithmetic#

The most basic arithmetic operations are addition and multiplication. Further operations such as subtraction, division and power are secondary as they can be reached by iteratively use the latter ones.

2.3.1. Addition#

import numpy as np
print("Error:", np.float32(5/7.+1/3.)-22/21.)

Error: 5.676632830464712e-08

Therefore, at the numerical computation level we must be aware that an expected zero result is really $$0\approx 10^{-16}$$

2.3.2. Multiplication#

For multiplication it is applied the same round-off rules as the addition, however, be aware that multiplicative errors propagate more quickly than additive errors.

N = 20
xe=1; x = 1
for i in range(N):
    xe *= float(2.0**(1.0/N))
    x *= np.float16(2.0**(1.0/N))
print('expected: {}; obtained: {}'.format(xe,x))

expected: 2.000000000000003; obtained: 1.9958053041750938

N = 20
xe=1; x = 1
for i in range(N):
    xe *= 2.0**(1.0/N)

np.float16(3.1415926535897932384626433832795028841971)

3.14

np.float32(3.1415926535897932384626433832795028841971)

3.1415927

float(3.1415926535897932384626433832795028841971)

3.141592653589793

np.float64(3.1415926535897932384626433832795028841971)

3.141592653589793

np.float128(3.1415926535897932384626433832795028841971)

3.141592653589793116

The final result has an error at the third decimal digit, one more than the case of addition.

2.3.3. ACTIVITY#

Find the error associated to the finite representation in the next operations

\[ x-u, \frac{x-u}{w}, (x-u)*v, u+v \]

considering the values

\[ x = \frac{5}{7}, y = \frac{1}{3}, u = 0.71425 \]

\[ v = 0.98765\times 10^5, w = 0.111111\times 10^{-4} \]

Computational Methods

Computer Arithmetics and Round-off Methods

Contents